Introduction to a Special Blog Series by NIST: “…How can we use data to learn about a population, without learning about specific individuals within the population? Consider these two questions:
- “How many people live in Vermont?”
- “How many people named Joe Near live in Vermont?”
The first reveals a property of the whole population, while the second reveals information about one person. We need to be able to learn about trends in the population while preventing the ability to learn anything new about a particular individual. This is the goal of many statistical analyses of data, such as the statistics published by the U.S. Census Bureau, and machine learning more broadly. In each of these settings, models are intended to reveal trends in populations, not reflect information about any single individual.
But how can we answer the first question “How many people live in Vermont?” — which we’ll refer to as a query — while preventing the second question from being answered “How many people name Joe Near live in Vermont?” The most widely used solution is called de-identification (or anonymization), which removes identifying information from the dataset. (We’ll generally assume a dataset contains information collected from many individuals.) Another option is to allow only aggregate queries, such as an average over the data. Unfortunately, we now understand that neither approach actually provides strong privacy protection. De-identified datasets are subject to database-linkage attacks. Aggregation only protects privacy if the groups being aggregated are sufficiently large, and even then, privacy attacks are still possible [1, 2, 3, 4].
Differential Privacy
Differential privacy [5, 6] is a mathematical definition of what it means to have privacy. It is not a specific process like de-identification, but a property that a process can have. For example, it is possible to prove that a specific algorithm “satisfies” differential privacy.
Informally, differential privacy guarantees the following for each individual who contributes data for analysis: the output of a differentially private analysis will be roughly the same, whether or not you contribute your data. A differentially private analysis is often called a mechanism, and we denote it ℳ.
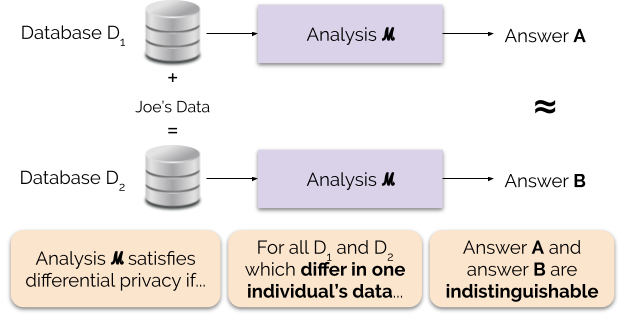
Figure 1 illustrates this principle. Answer “A” is computed without Joe’s data, while answer “B” is computed with Joe’s data. Differential privacy says that the two answers should be indistinguishable. This implies that whoever sees the output won’t be able to tell whether or not Joe’s data was used, or what Joe’s data contained.
We control the strength of the privacy guarantee by tuning the privacy parameter ε, also called a privacy loss or privacy budget. The lower the value of the ε parameter, the more indistinguishable the results, and therefore the more each individual’s data is protected.
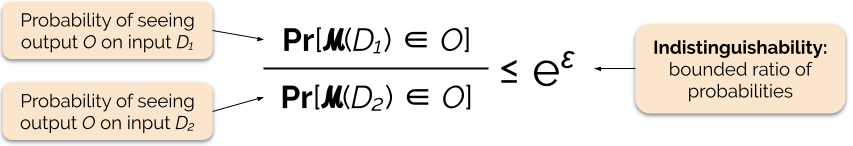
We can often answer a query with differential privacy by adding some random noise to the query’s answer. The challenge lies in determining where to add the noise and how much to add. One of the most commonly used mechanisms for adding noise is the Laplace mechanism [5, 7].
Queries with higher sensitivity require adding more noise in order to satisfy a particular `epsilon` quantity of differential privacy, and this extra noise has the potential to make results less useful. We will describe sensitivity and this tradeoff between privacy and usefulness in more detail in future blog posts….(More)”.