Article by Rob Goodman and Jimmy Soni: “Just what is information? For such an intuitive idea, its precise nature proved remarkably hard to pin down. For centuries, it seemed to hover somewhere in a half-world between the visible and the unseen, the physical and the evanescent, the enduring medium and its fleeting message. It haunted the ancients as much as it did Claude Shannon and his Bell Labs colleagues in New York and New Jersey, who were trying to engirdle the world with wires and telecoms cables in the mid-20th century.
Shannon – mathematician, American, jazz fanatic, juggling enthusiast – is the founder of information theory, and the architect of our digital world. It was Shannon’s paper ‘A Mathematical Theory of Communication’ (1948) that introduced the bit, an objective measure of how much information a message contains…
Shannon’s ‘mathematical theory’ sets out two big ideas. The first is that information is probabilistic. We should begin by grasping that information is a measure of the uncertainty we overcome, Shannon said – which we might also call surprise. What determines this uncertainty is not just the size of the symbol vocabulary, as Nyquist and Hartley thought. It’s also about the odds that any given symbol will be chosen. Take the example of a coin-toss, the simplest thing Shannon could come up with as a ‘source’ of information. A fair coin carries two choices with equal odds; we could say that such a coin, or any ‘device with two stable positions’, stores one binary digit of information. Or, using an abbreviation suggested by one of Shannon’s co-workers, we could say that it stores one bit.
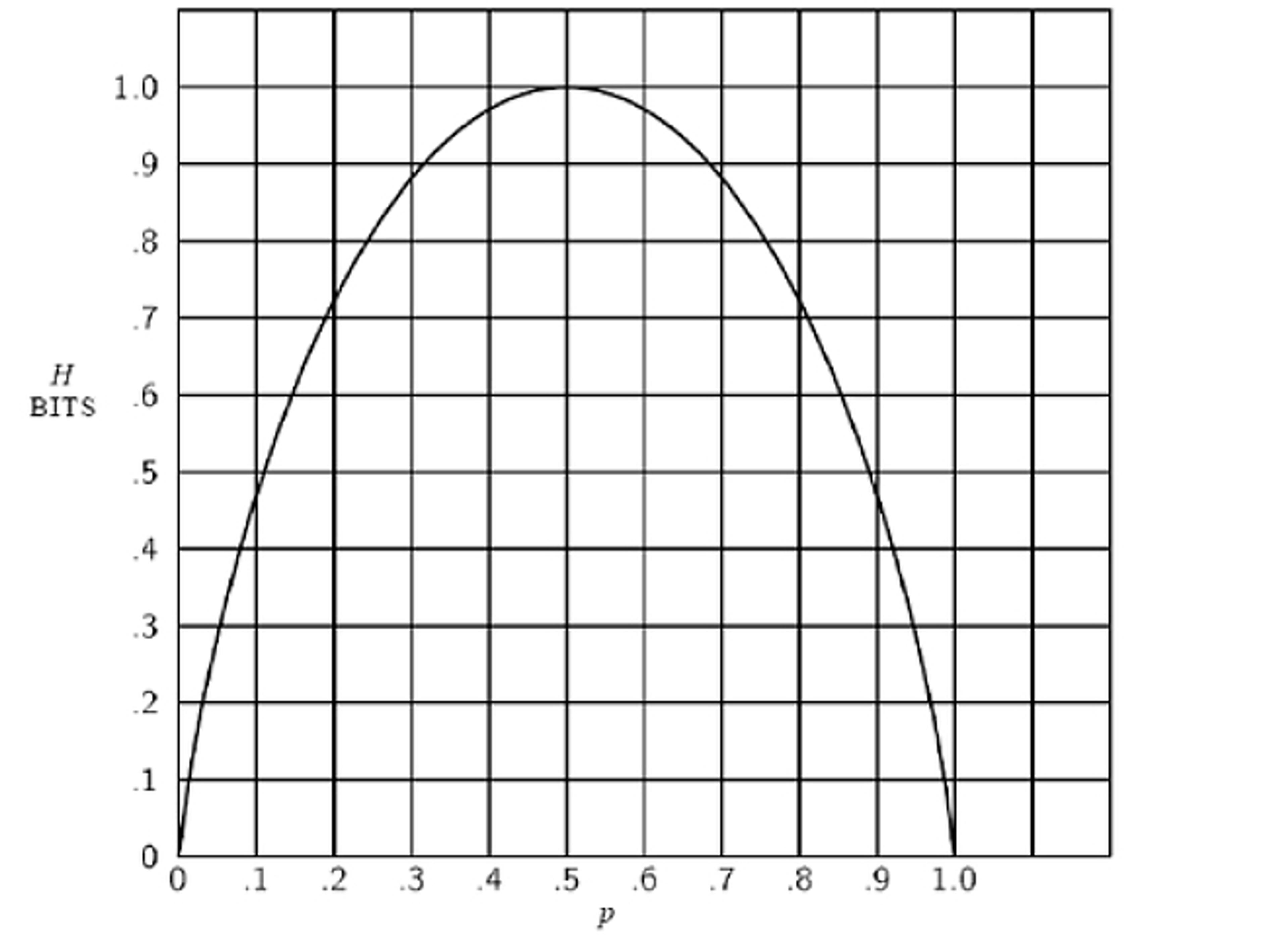
But the crucial step came next. Shannon pointed out that most of our messages are not like fair coins. They are like weighted coins. A biased coin carries less than one bit of information, because the result of any flip is less surprising. Shannon illustrated the point with this graph. You see that the amount of information conveyed by our coin flip (on the y-axis) reaches its apex when the odds are 50-50, represented as 0.5 on the x-axis; but as the outcome grows more predictable in either direction depending on the size of the bias, the information carried by the coin steadily declines.
The messages humans send are more like weighted coins than unweighted coins, because the symbols we use aren’t chosen at random, but depend in probabilistic ways on what preceded them. In images that resemble something other than TV static, dark pixels are more likely to appear next to dark pixels, and light next to light. In written messages that are something other than random strings of text, each letter has a kind of ‘pull’ on the letters that follow it…(More)”