Kelsey Houston-Edwards at Scientific American: “When you hit “send” on a text message, it is easy to imagine that the note will travel directly from your phone to your friend’s. In fact, it typically goes on a long journey through a cellular network or the Internet, both of which rely on centralized infrastructure that can be damaged by natural disasters or shut down by repressive governments. For fear of state surveillance or interference, tech-savvy protesters in Hong Kong avoided the Internet by using software such as FireChat and Bridgefy to send messages directly between nearby phones.
These apps let a missive hop silently from one phone to the next, eventually connecting the sender to the receiver—the only users capable of viewing the message. The collections of linked phones, known as mesh networks or mobile ad hoc networks, enable a flexible and decentralized mode of communication. But for any two phones to communicate, they need to be linked via a chain of other phones. How many people scattered throughout Hong Kong need to be connected via the same mesh network before we can be confident that crosstown communication is possible?

A branch of mathematics called percolation theory offers a surprising answer: just a few people can make all the difference. As users join a new network, isolated pockets of connected phones slowly emerge. But full east-to-west or north-to-south communication appears all of a sudden as the density of users passes a critical and sharp threshold. Scientists describe such a rapid change in a network’s connectivity as a phase transition—the same concept used to explain abrupt changes in the state of a material such as the melting of ice or the boiling of water.
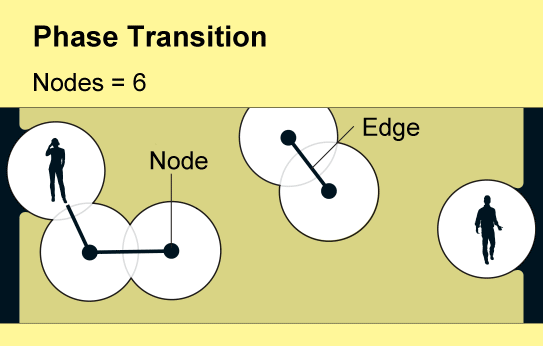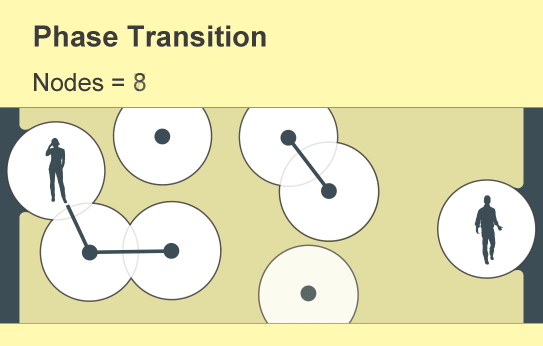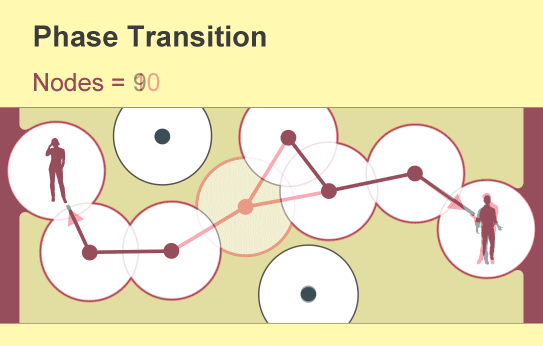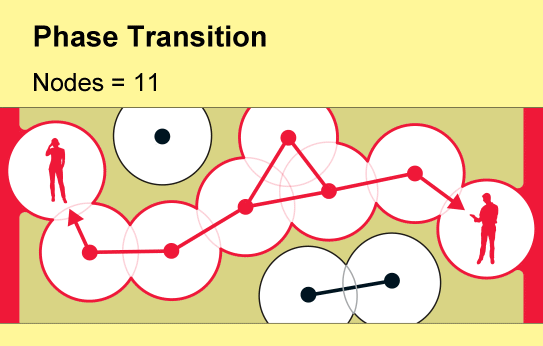
Percolation theory examines the consequences of randomly creating or removing links in such networks, which mathematicians conceive of as a collection of nodes (represented by points) linked by “edges” (lines). Each node represents an object such as a phone or a person, and the edges represent a specific relation between two of them. The fundamental insight of percolation theory, which dates back to the 1950s, is that as the number of links in a network gradually increases, a global cluster of connected nodes will suddenly emerge….(More)”.